资本资产定价模型(Capital Asset Pricing Model or CAPM)是收益法评估股权价值的常用模型,对于开展区间估计所需的收益误差参数,可以通过资产评估报告利用资本资产定价模型对标的企业股权收益风险的衡量参数来获取。哈里·马科维茨(Harry M. Markowitz,1952)提出了著名的“均值方差模型[1](Mean-Variance Model)”,该模型将证券组合收益率的分布合理假设为正态分布,以其期望和方差来描述期望收益率和波动风险。方差对风险的度量依赖于收益率相对于其期望的离散程度,离散程度越大,方差就越大,即投资组合的风险越大,这也是资本资产定价模型的理论基础。资本资产定价模型是由夏普(William Sharpe,1964)、林特纳(Jone Lintner,1965)和莫辛(Mossin,1966)等学者提出的。该模型认为标的企业未来每年的经营收益是一个服从概率分布的随机变量,而非一个确定值,同时这个随机变量服从正态分布。(2)理性的投资者将持有有效的投资组合(即完全多样化的投资组合);(3)所有投资者有相同的投资时间期限(即预期持有时期);(4)所有投资者对于预期收益率和折现率等变量产生过程有相同的预期;(6)不存在与投资相关的税收,但是可能存在企业收入税收;(8)市场具有完全的分割性和流动性(即投资者随时能够买入或者卖出任何希望的零散权益)。资本资产定价模型的提出早于有效市场假说,但其假设条件(投资者追求期望效用最大化以及同质性信念假设)与市场有效假说一致,本文中我们提到的市场均假设为强有效市场。尽管CAPM的基本假设在实践中可能不完全成立,但在收益法定价中仍广泛使用,CAPM模型提供了一个理论框架来解释在特定假设前提下一些特定关系是如何成立的,本文的后续分析仍在这一框架下进行。除了评估报告中的评估假设、限制条件和CAPM理论的假设前提,本文还有如下假设:(1)场是可靠的,市场超额收益率和市场波动率不是随机变量,而是可以通过一定方式确定的(通常是通过历史数据)。(2)标的公司收益率与市场收益率的相关系数可以通过历史数据确定。在选用收益法实施资产评估时,资产评估师通常考虑评估标的历史经营状况、行业生命周期和业务逻辑等因素,综合判断评估标的未来最有可能实现的收益。从统计学的角度看,这项资产评估活动的本质是对企业未来收益分布的期望值的估计,因此“评估师认可的企业收益水平是否符合企业实际收益水平”这一问题就可以抽象为实际收益是否落在上述分布函数参数估计的置信区间的问题。在数理统计学中,“参数估计”是指通过样本统计量对总体参数进行估计,具体包括“点估计”和“区间估计”两种主要形式。点估计的结论是一个精确值,不具备衡量估计精度的功能,而区间估计在点估计的基础上进一步估计出总体参数的分布区间,并给出总体参数落在这一区间内的概率分布情况。区间估计根据一定水平下的可信度要求,构造出适当的区间作为总体参数值分布范围的估计区间,即置信区间。当需要确定的置信区间为均值区间,收益的标准差已知(可推导)时,可以采用Z分布进行区间估计。
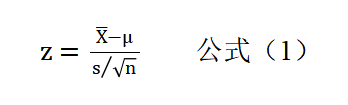
其中:
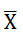 ——样本均值;
——样本均值;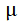 ——总体均值;
——总体均值;
s——样本标准差;
n——样本总量。
总体均值μ在1-α置信水平下的置信区间为:
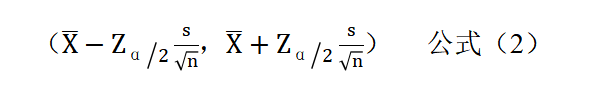
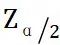 ——概率值为
——概率值为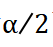 下的z分位数。
下的z分位数。那么,我们可以认为,期望值(预测值)落在置信区间内的概率为1-α。
资产评估师认可的企业管理层对未来经营收益的预测中,预测收益的含义是企业收益最有可能实现的数值,不是一定会实现的数值,基于CAPM理论中收益为服从正态分布的随机变量,未来收益最可能实现数则为该正态分布的均值;预测的风险则由正态分布的方差σ2表示,反映实际收益可能偏离期望收益的范围,在收益法评估中,这一风险在折现率中体现。因此,在收益预测和折现率已知的情况下,可以通过区间估计得到一定置信水平下预测收益的置信区间,这一置信区间即为评估师认可的收益预测合理区间。
利用上述统计学方法,可以对资产评估报告隐含的企业预测收益合理区间进行定量分析,也可以更加科学地判断企业未来收益的预测与实际收益水平的偏离程度。
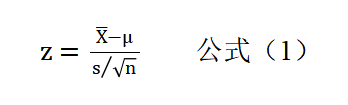
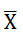 ——样本均值;
——样本均值;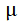 ——总体均值;
——总体均值;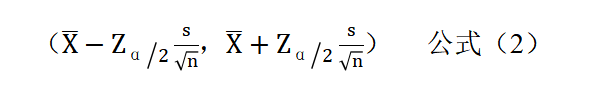
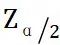 ——概率值为
——概率值为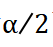 下的z分位数。
下的z分位数。
 English
English